# 数组和计算式 ↵

1 + 1, 3 * 2 就是所谓的计算式了，他是编程中表达式的一个真子集，运行它可以得到结果，比如运行 1 + 1 得到结果 2。

来观察如下的计算式：

00 1 + 2 + 3 + 4 + 5 
01[1,  2,  3,  4,  5]

可以发现，它可以跟数组一一对应，进一步来看，仅需再提供如下的 规则 就可以将数组跟计算式等价。

数组应该给出如何运算的函数。
计算从左到右结合。
计算式的括号，是嵌套的数组。

下面，我将分别讲述这三点。

# 数组应该给出如何运算的函数

对此，我们应该对数组进行一些修改，把函数提前，用字符串表示：

00['+', 1, 2, 3, 4, 5]

上述数组代表着 1 + 2 + 3 + 4 + 5, 是一种抽象

# 计算应该从左到右结合

这句话表明， + 只有两个参数，运算的时候，应该从左到右积上去。

像这样，它对应着 reduce 操作：

00[1, 2, 3, 4, 5].reduce(
01    (acc, cur) => acc + cur
02); // => 15

上述式子代表着 1 + 2 + 3 + 4 + 5 = 15 的求值过程。

# 计算式的括号，是嵌套的数组

是这样的：

00(1 + 2 + (1 + 2))
01['+', 1, 2, ['+' 1 2]]

括号代表又一个计算式，它是递归的，而数组本身天然就是可构成递归结构的，因此可以无缝结合。

# 数组计算式 ↵

像上面提到的形如 [’+’, 1, 2, 3] 可以叫做数组计算式

那么要如何运行求值一个 数组计算式 呢？经过考虑，有如下三个点：

数组计算式的第一个元素是 如何计算
计算的过程应该是剩余元素 reduce 的过程
数组计算式的元素也可以是数组计算式

考虑到第三点，需要用递归的方式去实现：

00let table = {
01    '+': (...args) => args.reduce((acc, cur) => acc + cur)
02}
03// let fn = table['+']
04// fn(1, 2, 3); 
05// => 1 + 2 + 3 = 6 
06
07let calc = exp => {
08    if (!Array.isArray(exp)) {
09        // 不是数组，是数字
10        // 则返回这个数字的计算结果即返回数字本身
11        return exp;
12    } else {
13        // 说明是数组 
14
15        // first 是 `+` 
16        // args 是剩余的参数 
17        let [first, ...args] = exp;
18
19        // 取出计算函数 
20        let fn = table[first];
21
22        // args 里的元素也可能是数组计算式 
23        // 递归的调用自己 
24        args = args.map(e => calc(e));
25        
26        // 最后进行 fn 的调用 
27        return fn.apply(null, args);
28    }
29}

计算结果

拓展 table，可以使其变得跟普通的计算式一样强大，我们甚至可以自定义运算符，仅需在 table 上编写函数即可。

# 变量和计算式 ↵

变量其实是一种映射，比如：

00// 这是变量池，里面存着变量名和对应的值 
01let vars = {
02    'a': -5 
03}
04
05// 在之前的 table 上拓展新的运算: 变量求值 
06table.find = var_name => vars[var_name]; 
07// let fn = table['find']
08// fn('a') 
09// => -5 
10
11// 要计算： 
12['+', 'a', 2, 3]; 
13
14// 其实就是： 
15['+', ['find', 'a'], 2, 3];

来看看执行结果：

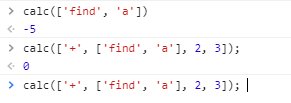
带变量的计算结果

结果为 0, 符合预期。

# 怎样写一个解释器 ? ↵

对于计算机的处理来说，数组计算式更好处理，对于我们人类来讲，普通的计算式更好理解。

解释器的一个工作是把普通的计算式解释为数组计算式，并吧变量的搜索附加上去，形成一种数据结构，如果这种数据结构是 汇编代码，那么这个解释器叫做编译器比较妥当，机器可以直接运行汇编码；如果解释成某种中间结构，那么还是叫做解释器，不过这种中间结构是可以求值的（比如上面提到的数组计算式就是一种中间结构），求值它需要一台抽象的机器，这台机器需要我们编程实现，它叫做虚拟机。

解释器的编写，有两大问题：

如何把源码（比如计算式）变成某种中间结构（比如数组计算式）
构造虚拟机对中间结构进行求值（这里的 calc 函数就是虚拟机）

而当中最有趣的，是第二点，构造虚拟机运行这种中间结构。

对了对了，忘记说了，本篇的数组计算式这个名字是我瞎说的，它的学名应该叫做 S 表达式，是构造解释器的时候很重要的一种数据结构，它是一种可迭代的递归结构，刚好跟数组对应，因此可以用数组去表达一个 S 表达式。