好吧我开坑做解释器了 … 准备做 Q 语言 … 额 … 实现变量、表达式、函数就 OK 了。
不知道接下来的有没有时间做，现在完成了表达式的解析，接下来应该要完成剩下的 变量、函数

不要报太大希望，Q-lang 可比 BASIC 糟糕多的多的多 …

解释器就是… 可以把一段文本当作 某种语言 解释执行，比如没有 V8 前的 JS 都是用解释器运行的，速度较慢，有了 V8 之后就先编译成中间格式，运行的时候速度块很多。

既然要做解释器，首先得实现解析 表达式

表达式的选择有很多种，我钦点了 S-表达式 作为解释器解释的表达式。

# 什么是 S-表达式 ↵

S-表达式是一种数据结构表示法 用文本表示一个数据结构
S-表达式被大量应用在 Lisp 里面

通过上述的描述你可能还不太清楚，我举例子把。

比如

把 1 + 1 写成 (+ 1 1)
把 (2 * 5) + 2 写成 (+ (* 2 5) 2)
把 1 + ((2 * 5) * (3 * 5)) 写成 (+ 1 (* (* 2 5) (* 3 5)))

这种把 操作符 提前的算式写法就叫做 S-表达式

这里写的解释器只能解释 S-表达式

# 为什么选择 S-表达式 ↵

为了更方便的把表达式解析成 AST 因此采取了 S-表达式
受王垠的博文启发才做的，因此采用跟他一样的设计思路

上面提到了 AST 这里得解释一下。

AST 全名是 抽象语法树，是 Abstract Syntax Tree 的缩写，可以认为它是 S-表达式所对应的数据结构，可以把以字符串显示的 S-表达式 转化成 AST 的过程叫做 Parse ，如图：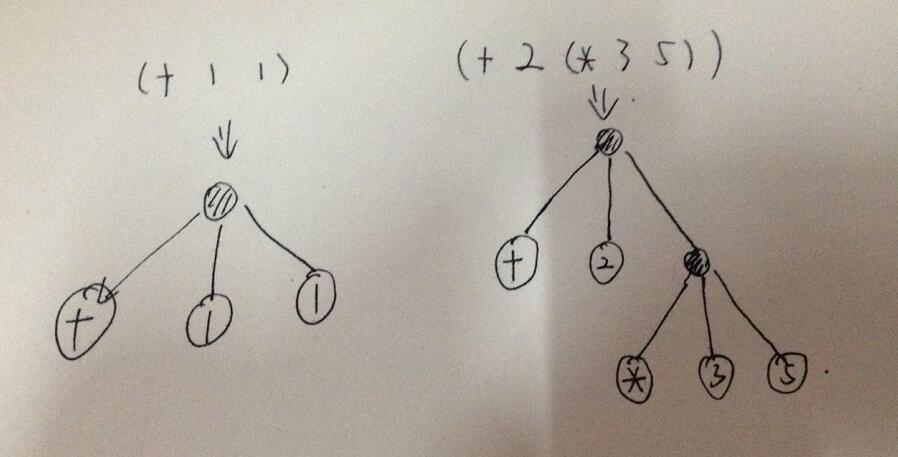

S-Expression => AST

其中非叶子节点（就是黑色斜线的那些节点）称作 子树

通过遍历这颗树，可以很方便的把全部 子树 的值求出来，也就是求得 S-表达式的值。

上述遍历用递归来写就是：

求当前子树的值
取得 子树 的操作符
取得操作符的左值和右值
如果左值是 子树 那么求左值的值得到左值 (递归调用第一步)
如果右值是 子树 那么求右值的值得到右值 (递归调用第一步)
把左值右值应用到操作符上即为当前子树的值

因此求的 (+ 2 (* 3 5)) 的过程就是：

求 (+ 2 x) 的值，因为 x 是子树所以求 子树x 的值。

求 子树x 的值即求 (* 3 5) 的值，因为左值右值都不是子树，所以可求得该子树的值是 15

回到 (+ 2 x) 的求值，左值已经求出，是 2，右值刚刚得出是 15，把 2 和 15 应用到 + 上可得结果 17

# 把 S-表达式解析成数组形式 ↵

要得到 AST 首先得把多余的空格去掉，把表达式中的元素抽离出来。

比如
(+ 1 1) 应该变成 ["(", "+", 1, 1, ")"]
(+ 1 (* 2 3)) 应该变成 ["(", "+", "1", "(", "*", "2", "3", ")", ")"]

看起来问题变复杂了，其实不然，因为语义元素分离出来了，我们就可以遍历数组来构造树了。

以下是我的做法：

00export const parseToArr = str => (
01    str.trim()
02        .split(' ')
03        .filter(e => e !== '')
04        .map((e, idx, its) => {
05            let temp = parseInt(e); 
06            if (Number.isNaN(+e)){
07                if (Number.isNaN(temp)){
08                    return e.split(''); 
09                } else {
10                    // e 可能是 "4))" "-4))" 这种 有带正负 
11                    const _ = e.replace(temp.toString(), '').split('');
12                    return [temp].concat(_);
13                }
14            } else {
15                return temp; 
16            }
17        }).reduce((acc, cur) => {
18            if (Array.isArray(cur)){
19                return acc.concat(cur); 
20            } else {
21                acc.push(cur); 
22                return acc; 
23            }
24        }, [])
25);

上述不是最佳的做法，最佳的算法我还在考虑。

以下是简单的测试用例

00import { parseToArr } from './parse-to-arr';
01
02var a = parseToArr('(+ 1 1)')
03  , b = parseToArr('(+ (* 2 3) 2)')
04  , c = parseToArr('(+ (* 2 3) (+ 1 1))'); 
05
06console.log('a:', JSON.stringify(a));
07// => a: ["(", "+", 1, 1, ")"]
08console.log('b:', JSON.stringify(b));
09// => b: ["(", "+", "(", "*", 2, 3, ")", 2, ")"]
10console.log('c:', JSON.stringify(c));
11// => c: ["(", "+", "(", "*", 2, 3, ")", "(", "+", 1, 1, ")", ")"]

parseToArr 的测试用例

结果正常继续。

# 把数组 parse 成 AST ↵

分析数组，并取出子数组：操作符组、左值组、右值组
如果左值组、右值组都是常数，把他们应用到操作符上即可求得这个数组的值否则执行下两步
如果左值组是常数，把左值应用到操作符，否则调用第一步来分析左值组并求得左值应用到操作符
如果右值组是常数，把右值应用到操作符，否则调用第一步来分析右值组并求得右值应用到操作符

为了实现操作符到函数的映射，我写了 rules 对象

00export const rules = {
01    '+': ap => bp => ap + bp, 
02    '-': as => bs => as - bs,
03    '*': am => bm => am * bm,
04    '/': ad => bd => ad / bd
05}

下面这段代码用来测试一下上面的 runles:

00import { rules } from './rules';
01
02const p = rules['+']; // 柯里化的加法
03const s = rules['-']; // 柯里化的减法
04
05console.log(p(5)(12)); // 5 + 12 => 17 
06console.log(s(14)(3)); // 14 - 3 => 11

然后递归实现 AST 的生成 (parse.js)：

00import { rules } from './rules';
01
02// 注意 parse 这里有下划线 
03// 这段代码暂时用不到 
04export const _parse = arr => {
05    var tree = Object.create(null)
06      , LR = []
07      , posStart = []
08      , posEnd = []
09      , deep = 0;
10
11    // posStart 代表左值括号的开始位置 
12    // posEnd 代表右值括号的结束位置 
13    // deep 代表括号嵌套的深度 
14    // 利用 deep 来判断括号的深度，以此区分出最外层左值 最外层右值 
15    // 比如 "(+ 1 (+ 1 (+ 2 3)))" 这里左值是 1 右值是 (+ 1 (+ 2 3)) 利用deep可以区分不同深度的括号 
16    // LR 代表左右值 （如果是常数）
17    // 比如 (+ 1 2) 的 LR 是 [{ val: 1, idx: 在数组的位置}, {val: 2, idx:在数组的位置}] 
18    // 如果是 (+ 2 (+ 3 4) LR 是 [{val: 2}, idx: 在数组的位置}] 
19
20    arr.forEach((ch, idx) => {
21        if (ch === '('){
22            // 加深度 
23            deep ++; 
24            if (deep === 2){
25                // 如果深度刚刚从 1 跳到现在的 2 
26                posStart.push(idx); 
27            }
28        } else if (ch === ')'){
29            // 减深度 
30            deep--; 
31            if (deep === 1){
32                // 如果深度刚刚从 2 跳到现在的 1  
33                posEnd.push(idx); 
34            }
35        } else if (rules[ch]){
36            if (deep === 1){
37                tree.o = ch;    
38            }
39        } else {
40            // 普通的数字 
41            // val 是值 pos 是这个值在数组中的位置 
42            if (deep === 1) LR.push({
43                val: ch,
44                pos: idx
45            }); 
46        }
47    }); 
48
49    if (LR.length === 0){
50        // 左右均为表达式
51        tree.a = _parse(arr.slice(posStart[0], posEnd[0] + 1));
52
53        tree.b = _parse(arr.slice(posStart[1], posEnd[1] + 1));
54    } else if (LR.length === 1){
55        // 左边是表达式、右边是数字
56        // 或者 
57        // 左边是数字、右边是表达式
58        let temp = LR.pop(); 
59        let l = posStart[0]
60          , r = posEnd[0];
61
62        // 如果 temp.pos 在 l 的左侧 那么 temp 是左值无误 
63        // 如果 temp.pos 在 r 的右侧 那么 temp 是右值无误 
64        if (temp.pos < l){
65            // temp 在左 
66            tree.a = temp.val; 
67            tree.b = _parse(arr.slice(posStart[0], posEnd[0] + 1));
68        } else if (temp.pos > r) {
69            // temp 在右 
70            tree.a = _parse(arr.slice(posStart[0], posEnd[0] + 1));
71            tree.b = temp.val; 
72        }
73    } else if (LR.length === 2){
74        // 左右均为数字 
75        tree.a = LR[0].val; 
76        tree.b = LR[1].val; 
77    } 
78
79    // 调试输出 
80    console.log('_parse.js:', JSON.stringify(arr));
81
82    return tree; 
83}

这里我觉得很蛋疼了。。可能能力不足把。勉强实现了。看王垠的代码很精简，不懂 Scheme 所以看不懂。。。只能自己慢慢实现绕了好几个坑才抓到这个方法用于解析 AST

以下是简单的测试用例 parse-test.js

00import { _parse } from './parse';
01import { parseToArr } from './parse-to-arr';
02
03// S-表达式 数组 
04['(+ 1 2)', '(+ (+ 1 2) 3)', '(+ (+ 1 2) (+ 3 4))']
05    .map(parseToArr)   // 映射成 S-表达式 数组
06    .map(_parse)       // 映射成 AST
07    .forEach(AST => {  // 打印出来 
08        console.log(AST); 
09    });

解析结果

其中 (+ (+ 1 2) (+ 3 4)) 的结果是：

00var AST = {
01    "o":"+",
02    "a":{
03        "o":"+",
04        "a":1,
05        "b":2
06    },
07    "b":{
08        "o":"+",
09        "a":3,
10        "b":4
11    }
12}

它无疑是一棵树，而且结构也是我们想象中的那样是递归的结构。

# 递归遍历 AST 求值 ↵

从上面的讨论中可以从以字符串显示的 S-表达式得到 AST 了，现在只需要遍历 AST 就可以得到结果。

遍历过程用代码描述很简单：

00import { rules } from './rules';
01
02export const calc = tree => {
03    let o = rules[tree.o]
04      , a = tree.a
05      , b = tree.b
06      , a_is_num = typeof a === 'number'
07      , b_is_num = typeof b === 'number';
08
09    if (a_is_num && b_is_num){
10        // a b 都是数字 说明已到达最深处 
11        return o(a)(b); 
12    } else if (!a_is_num && b_is_num) {
13        // a 是表达式, b 是数字 继续对 a 求值 
14        return o(calc(a))(b); 
15    } else if (a_is_num && !b_is_num) {
16        // a 是数字, b 是表达式 继续对 b 求值  
17        return o(a)(calc(b)); 
18    } else if (!a_is_num && !b_is_num){
19        // a b 都是表达式 都要继续求值 
20        return o(calc(a))(calc(b)); 
21    }
22}

以下是测试用例

00import { _parse } from './parse';
01import { parseToArr } from './parse-to-arr';
02import { calc } from './calc';
03
04['(+ 1 2)', '(+ (+ 1 2) 3)', '(+ (+ 1 2) (+ 3 4))'].forEach(rawCode => {
05    console.log('Do Calc For', rawCode);
06    const arr = parseToArr(rawCode);
07    const ast = _parse(arr);
08    const result = calc(ast);
09    console.log(rawCode, '==>', result);
10    console.log('======');
11});

执行结果

结果如预期所想

# 最后的封装 ↵

最后封装一下从字符串到数组再到AST再到值的过程：

00import { _parse } from './parse';
01import { parseToArr } from './parse-to-arr';
02import { calc } from './calc';
03
04// 注意parse这里没有下划线 
05export const parse = str => _parse(parseToArr(str)); 
06export const Q = str => calc(parse(str)); 
07
08// Q('(+ 1 1)')       ===> 2 
09// Q('(+ 2 (* 2 3))') ===> 8

简单的执行

现在我们得到的 Q 就有点类似于 eval 了，接下来要实现变量、函数等特性，请见下一篇博文。

# live demo ↵

这里我已经完成了代码，请直接运行下面的代码框即可运行。

00require('./demo.jsx');
01// 👇 运行 Run !

此处为上面这个 demo 的源码，点我展开

00import { Q } from './q';
01import React from 'react';
02import ReactDOM from 'react-dom';
03
04window.Q = Q;
05console.log('Q inited');
06
07function App() {
08    const [result, setResult] = React.useState('');
09
10    return (
11        <div>
12            <div>请在下面的输入框中输入 S 表达式</div>
13            <input id="_s-exp" defaultValue="(+ 1 2)" type="text" placeholder="输入S表达式" />
14            <button id="to-calc" onClick={() => {
15                const $ = document.getElementById('_s-exp');
16                if (!$) console.log('error');
17
18                setResult(Q(document.getElementById('_s-exp').value));
19            }}>点我开始计算</button>
20
21            {result ? <div>结果为: { result }</div> : null}
22
23            <br />
24        </div>
25    );
26}
27
28ReactDOM.render(<App />, document.getElementById('demo'));

# Links ↵